the tractors which
plough
In Europe during the Middle Ages, and in China and India until quite
recently, something like eighty per cent of all human labour was devoted to
the production of food — a situation which persists in some parts of the
world even today. In the industrial countries, by contrast, the figure is
five per cent or less, and just as importantly, the proportion of
back-breaking stoop labour is likewise reduced. Where farmers plant or
harvest their fields in air-conditioned comfort, it scarcely seems to be
claiming too much to say that we have lifted the curse of Adam.

The atom must be
democratized.
I regret
nothing!
Atomic Energy Primer
For the description and development of atomic theory, your author is indebted to Horace Deming, General Chemistry (Fourth Edition Rewritten and Revised, New York, John Wiley & Sons, 1935), especially Chapters III (“Weight Relations and Chemical Change”) and IV (“Molecules and Atoms”).
daltons (Da)
The dalton, also known as the “unified atomic mass unit”, is by definition
12 g / (12 × NA), or within the limits of
present-day measurement, 1.660 538 923×10−27 kg.
The electron-volt is a minuscule unit used in nuclear physics, the energy
imparted to a single electron by an electromotive force of one volt, equal to
1.602×10-19 joules. One dalton is the Einstein equivalent of 931.5
million eV.
The curve of binding
energy
Given an species R, having atomic number ZR and mass number
MR, we can define a putative atomic mass : PR =
(ZR × mP)
+ ([MR - ZR]
× mn)
= (ZR × 1.007825) +
([MR - ZR] × 1.008655) [Da]
where mP is the mass of a neutral hydrogen atom,
and mn is the mass of a free neutron. If the
actual mass of the atom is mR, the mass defect
DR and the mass defect per nucleon dR are then :
DR =
PR - mR
dR = DR / MR It is
important to recognize that dR is an average over all the nucleons
of R, and that in the theoretical operation of assembling a nucleus of R from
free protons and neutrons, the binding energy contribution of each successive
particle would be different. For mass numbers in the range of about 30 to
180, however, at reasonable proton-neutron ratios, the average binding energy
per nucleon clusters around 8.5 MeV, and so the change in binding energy
associated with adding or removing a nucleon will be about that much.
The maximum energy available from any possible nuclear transformation of R
can be calculated by comparison with the nucleus having the greatest mass
defect per nucleon, which we will symbolize by a subscript zero. ΔEmax =
MR × (dR - d0)
= DR -
([MR / 62] × D0) This is the
energy, per atom of R, which one would obtain by taking an indefinitely large
number of such atoms, separating them into their constituent particles,
allowing beta or inverse-beta decays to occur as necessary to correct the
neutron-proton ratio, and then recombining the resultant particles to make
neutral 62Ni atoms. Pretty much any real nuclear transformation or
series of transformations will give up somewhat less than this.
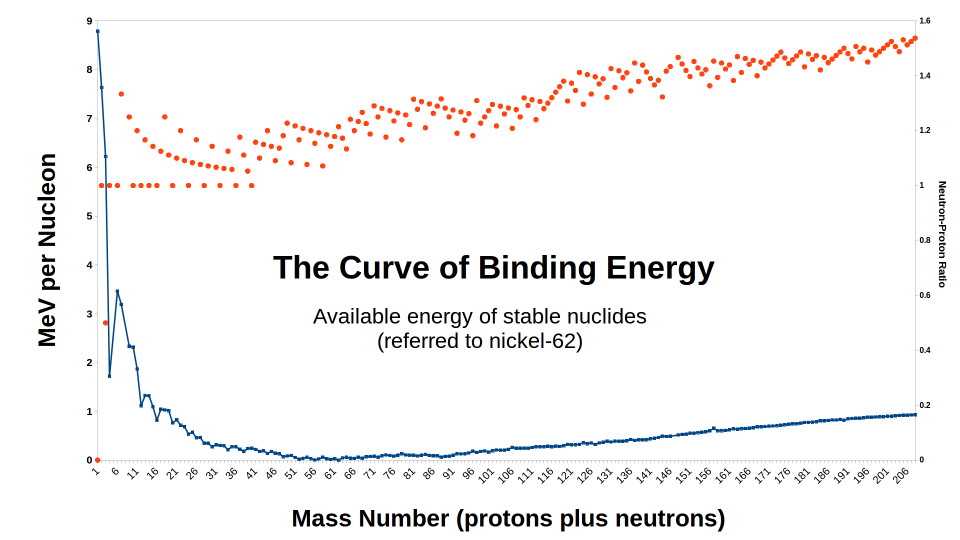
As an almost
invariable rule…
An exception appears to occur in the case of certain beta (including
positive-beta and electron-capture) decays, for which the ‘pressure’ exerted
by the electrons of the atom influences the energy balance of the nuclear
transition. Thus the half-lives of tritium, beryllium-7, and technetium-99
vary slightly with their states of chemical combination. As an extreme case,
it has been
proposed [PDF, 1.1 MB] that thallium-205 becomes radioactive when the atom
is fully ionized, ie, has been stripped of all its eighty-one electrons.
Neutrinos, which are known to cause beta-decay-like transitions on the rare
occasion they interact with stable nuclei at all, may also influence the decay
rates of nuclei unstable with respect to beta decay, although this phenomenon
is less well-established. Neither alpha decays, nor the internal transitions
which produce gamma emission, exhibit any such effect.
The mass of this
quantity of any radioactive species…
The formula is mBq =
(T½ × M) /
(NA × ln[2]) =
(T½ × M) / 4.174×1023
where T½ is the half-life in seconds, M is the
molar mass, and NA is Avogadro’s number. Recall that
M = m × NA, where
m is the atomic mass ; by definition, the numerical
values of M (in grams per mole) and m (in
daltons) are the same, but the mass of one becquerel in dalton units is not
often required.
Note also that the ‘tropical year’ of 31 556 926 seconds should
properly be used for conversions, although the error resulting from the use of
the ‘calendar year’ of 31 536 000 seconds is ordinarily negligible.
The reciprocal of the becquerel mass mBq by this
formula is the specific activity in becquerels per gram.
…a definite tendency
to absorb neutrons
While a proton will capture a neutron to become a deuteron, a deuteron may
be broken up by a gamma ray. (The same phenomenon is observed with
beryllium.) So, any water-moderated reactor should ultimately (over the
course of centuries, perhaps) attain an equilibrium isotopic composition,
where the ‘neutron-absorption cross section’ of protium, multiplied by the
neutron flux, is equal to the ‘photoneutron cross-section’ of deuterium,
multiplied by the γ flux. If no other source were available, a light-water
reactor could in principle be used for the production of deuterium.
The photoneutron effect is of importance in the operation of
heavy-water-moderated fission reactors, because gammas are produced both while
fission is ongoing, and after shutdown by the continued decay of fission
products. Procedures and control mechanisms must take into account the
resulting addition of neutron flux.
…paired with
standard combustion-turbine components…
A steam power system, because of its complexity, incurs higher capital,
operation, and maintenance charges than a gas-turbine system of the same
output rating. For this reason, it can be cheaper to generate power from
natural gas using a turbine plant than from coal using a steam plant, even
when the price of gas per unit fuel value is considerably higher. Since the
variable cost of heat from any nuclear system of reasonable design is
extremely cheap, it makes sense to concentrate on lowering the fixed
cost of the energy-conversion plant, in order to reduce the total cost of
power. Combustion gases, of course, are mostly air, and air is mostly
nitrogen.
Radiation Safety and Atomic Power
For extensive coverage of the sources and effects of exposure to radiation and radioactivity, reference should be made to the publications of the United Nations Scientific Committee on the Effects of Atomic Radiation. The following precis should assist in understanding the biological significance of the various forms of radiation, including the relative biological effectiveness factors on which the sievert is based, and the limits on various kinds of exposure.
- α
- Alpha particles carry a great deal of energy, but slow down very quickly in almost all media. Because they cannot penetrate the outermost layer of the skin, or a few centimeters of air, they are scarcely dangerous unless emitted inside the body. Alpha-active nuclides, then, are considered primarily ingestion or inhalation hazards, unless they also have strong γ emission.
- β
- Beta (and β+) particles are more penetrating than α for a given kinetic energy, but there are few really energetic β emitters with half-lives more than a few seconds. External β exposure can cause severe but superficial burns ; ingestion or inhalation are again the main avenues of concern for exposure.
- γ
- Because the photon carries no charge, γ rays are less effective (for a given energy) at producing ionization than α or β particles, but by the same token they are much more penetrating. The more powerful gammas can pass virtually unimpeded through shields which would block all the alphas and betas, and they produce ionization in tissue along straight-line paths.
- Neutrons and others
- The effects of neutrons are somewhat hard to separate from the other
radiations which normally accompany their production. A neutron, being
uncharged, is itself not ionizing ; the principal mechanism of damage,
at least in living tissue, is the ejection of protons from molecules by
recoil, although gammas from absorptions and inelastic collisions may also
become significant. Perhaps the greatest ever one-time dose of pure fast
neutrons was received by physicists Luis Alvarez and Alvin Weinberg, owing to
carelessness in operation of a large cyclotron. Alvarez lived another five
decades, ultimately dying of cancer at age seventy-seven, a fate observed in
plenty of men who did not spend decades in radiation laboratories, while
Weinberg, four years younger, lived to be ninety-one. Exposure to large
radiation doses from prompt criticality accidents has been observed to cause
cataracts in the eyes, which are considered attributable to neutrons.
- Probably the most dangerous radiation is the so-called cosmic rays, especially those known as galactic primaries. Cosmic radiation, as its name implies, comes from space ; some of it consists of protons from the Sun, but the origin of the rest is somewhat obscure. Collisions between ‘primary’ cosmics and the atoms of the atmosphere result in ‘secondary’ cosmics, including particles such as muons, which can cause nuclear reactions (whence the ‘cosmogenic’ radionuclides such as tritium and 14C). The galactic primaries are heavy ions, up to and including iron, moving at very large fractions of the speed of light. Like α particles, they are very efficient at producing ionization, but unlike alphas, they have so much energy that they are not easily stopped. Aside from being the reason that passenger aviation is a significant source of global radiation exposure, the cosmic rays are a serious concern for long-duration spaceflight.
- Internal versus External
- Some people seem to believe that there is an inherent difference between
radiation from sources outside the body, and radiation from within the body.
In fact, as we have seen, the damage is done when the particle or ray passes
through tissue, so where it originates is not immensely important. The key
point about internal sources is that one carries them around, giving more time
during which exposure can occur.
- Some radioisotopes, because of their chemical properties, pass rapidly through the body or are never absorbed in the first place, but others have some affinity for a particular tissue, where they take up residence with results of special importance. Thus, as much of the iodine in the body is concentrated in the thyroid gland, this is the organ endangered by ingestion of 131I (whence the administration of radioinert iodine preparations to flush the radioactive material from the body), and strontium-90 will migrate to the bones because of its similarity to calcium, making it a danger for bone cancer. On the other hand, despite its curious reputation for deadliness, plutonium is not excessively dangerous when inhaled as a dust, because it oxidizes rapidly to a form which does not dissolve in body fluids, and such particles as are trapped in the lungs encyst themselves in a layer of dead cells which then shield the live tissue against α radiation.
So, for instance,
we read…
On pages 202-203 of Shippingport Operations With the Light Water
Breeder Reactor Core, DOE
Research and Development Report WAPD-TM-1542 (Bettis Atomic Power
Laboratory, March 1986) [PDF, 11 MB]. “During the second quarter of 1983, a
total of 103,750 gallons of processed water, with 0.000009 curies of
cobalt-60, was discharged.” This was during the decommissioning
procedure ; small quantities of radiocobalt were present owing to
neutron bombardment of impurities in the steel and zirconium-alloy of the
reactor and fuel assemblies. The 5.26-year half-life of 60Co, it
should be observed, is ephemeral compared to natural radioactives such as
226Ra (1600 years).
…the magazines in a small library.
According to Paul Frame of Oak Ridge, a glossy magazine typically contains
about 26
becquerels per kilogram of naturally-occurring radioactives. Thirteen
copies, a quarter of a year, of Aviation Week and Space Technology
from the 1960s (including one double issue) which the present author had on
hand came to 3.2 kg. Some magazines are weekly, some monthly, some quarterly,
but on average 3 kg (78 Bq) per title per year would not be a bad estimate.
333 kBq would then be 4286 title-years, or a fifty years’ run of 86 titles, a
few shelves of bound volumes. Actually, this is probably a high estimate,
because if processing strips out the lower members of the thorium series, a
‘fresh’ magazine will be considerably less radioactive than one which has
stood for a few years.
…if general
population exposure followed the same pattern.
The 1993 UNSCEAR estimate was that electricity production from coal
resulted in a global collective dose of 20 Sv per gigawatt-year, and from
fission, 3 Sv/GW·a, or about seven to one. Coal is also burned in industrial
and domestic settings, but if we may validly generalize from this figure,
total exposure from coal would be be 37.6 times exposure from fission, and the
reduction from a total substitution of fission for coal would be 32 times the
present exposure from fission.
A collective dose estimate of 200 Sv/GW·a over ten thousand years for
fission was also presented ; although the principal source was
identified as radon generated by 226Ra and 230Th left
behind in mine tailings, no such long-term estimates were made for any other
activity which distributes long-lived natural radioactive material. Coal
wastes would seem a comparable source. Even assuming that this value has any
real meaning, the use of breeder reactors (which should produce 100 or more
times the energy from the same amount of mined fuel) and thorium (which has no
long-lived daughter products to serve as source terms) would bring it down
sharply.
A more complete evaluation of exposure from various types of electricity
generation is expected from the 61st session of the UNSCEAR, held in July
2014.
Thorium and the nuclear fuel cycle
…this poses no
insuperable problems.
In thorium under neutron irradiation, protactinium is continuously being
formed, and two processes are competing to remove it : beta decay to
233U, with a half-life of 27 days, and neutron capture. At high
neutron fluxes, capture predominates, and an equilibrium concentration is
established where the rate of formation by captures in thorium is equal to the
rate of removal by captures in protactinium. Since the ‘thermal neutron
capture cross-section’ of 232Th is 7.4 barns (a jocularly-named
unit, 10-28 m2), and that of 233Pa is 43
barns, the concentrations will be in the inverse ratio, 85% Th and 15% Pa.
(This neglects the effect of the intermediate product, 233Th,
half-life 22 minutes, capture cross-section 1500 barns.) Where flux is low,
the equilibrium concentration of protactinium is lower, and 233U
accumulates.
The observed effect is that, in a solid-fuel reactor, the fissile material ‘migrates’ from areas of high flux to areas of low flux, and the overall reactivity becomes less for geometrical reasons, until the chain reaction can no longer be maintained. At this point, the fuel must be reprocessed and refabricated, which incurs significant costs. As a result, we can reasonably say that, for the typical LWR, fuel is expensive and neutrons are cheap — whence the use of ‘burnable poisons’ such as boron and gadolinium to control power distribution and increase fuel life — while for the LWBR, the opposite is true. Thorium is less costly than natural, not to speak of enriched, uranium, but its utilization demands that the minimum of neutrons be allowed to escape, or be absorbed by some competing nuclide.
If the fuel elements are ‘shuffled’ between high-flux and low-flux regions, so that protactinium is allowed to form rapidly and then decay, the interval between reprocessings can be extended. Shuffling is practiced in LWRs, but it requires shutting down the reactor for an extended period so that the vessel can be opened. In a CANDU or AGR operated as a thorium breeder, this is not necessary. A fuel element might, for instance, be irradiated to protactinium equilibrium, then removed from the reactor and allowed to cool for ninety days. At this point, about 90% of the protactinium would have decayed, and the uranium concentration would therefore be 13% — considerably enriched.
In practice, formation of 234Pa and 235U, and other side-processes, would become significant at such high 233Pa levels. As a general statement, however, it appears that reasonably frequent shuffling of fuel elements, with some out-of-core holding period, especially when combined with the high inherent neutron efficiency, would permit either CANDU or AGR thorium breeders to attain very high burnups. The limiting factor would be the buildup of stable or long-lived neutron-absorbing fission products.
Atoms for Peace, and Profit
A kilogram of
fissile material…
These figures are for the fission of 235U, which has an atomic
mass of 235.0439 Da, giving a total of 2.56×1024 fissions per
kilogram. 200 MeV is a very rough average, but if we assume that the energy
scales with the number of nucleons involved, then each fission of
233U would give 1.01 times as many fissions per kilogram
(235.0439/233.0395), 0.992 times as energetic (234/236), which is 1.000 ;
239Pu, 239.0522 Da, 0.983 fissions 1.02 times as energetic, which
is likewise 1.000. So, the fuel values of the three fissile nuclides are
effectively the same.
There are, of course, other directions from which an analysis of the value
of fissile material might be made, but this one seems to be, at the least,
indicative.
Renewables versus Demand
capacity
factor
More rigorously : If the rated power of a device or system is P, and
the energy actually produced or handled by it over a time interval T is E,
then the average power is P̅ = T / E
and the capacity factor isκ = P̅ / P
Letting δ be the duty cycle, or the fraction of T that the device or system is
in operation, we can also define an occupancy factor : ω = κ / δ
In the specific context of power generation, assuming that we want to serve
a constant load L using an intermittent source of rated power P, and a storage
mechanism with a round-trip efficiency (joules out divided by
joules in) of η and a rated (input or output) power Q, it is reasonable to
derive the following relations : Q = L ×
(1 - δ) / (δ × η)
P = (1 / ω) × (L + Q) =
(L / ω) × (1 + [{1 - δ} /
{δ × η}])
Storage capacity S is determined by the period τ over which the flow of power
is to be averaged : S = τ × Q ×
δ = L × τ × (1 - δ) / η The limiting
cases are ‘all-or-nothing’ generation, in which the intermittent source
operates only at its full output, ω = 1, and the converse, which
occurs if the source somehow happens to produce at fraction κ of its rated
power all the time, ω = κ (and S = 0), so that P =
L / κ. As the phenomenon of a ‘dead calm’ is familiar even in the
windiest of areas, and every terrestrial solar collector is subject to
something known as ‘night’, this latter is scarcely to be encountered.
The case in which the load varies with time is substantially more complex,
especially as it is necessary to consider whether its variation is correlated
with the variation of output, but it is reasonable to use the constant-load
case to gain a general understanding of the problem. After all, a
time-varying load can generally be decomposed into a constant term and a
variable term ; the former is known as the ‘baseload’, and is a
practical matter of great importance.
To illustrate things more concretely, suppose we want to serve 1 GW of
demand with wind machines having an average capacity factor of 30% (about the
highest figure encountered in practice) and pumped-hydroelectric storage
having an efficiency of 80% (definitely on the high side). Then, if the wind
machines run at 100% power 30% of the time, we need 1000 MW of generation to
serve the demand while the wind is blowing, and another 2900+ MW to feed the
storage (which, of course, has to be rated to handle that much power). We
arrive at that figure by observing that the power flow out of the storage
needs to be 1 GW 70% of the time, so, during the remaining 30%, the power flow
in needs to be sufficient to replenish that, plus account for the 20% loss.
On a twenty-four hour basis, in other words, generation is going on for 7.2
hours, both to meet the current demand, and to store enough power to provide 1
GW continuously during the remaining 16.8 hours. Supplying the required 24
gigawatt-hours per day means storing (16.8 / 0.8) or 21 GWh, and the
total required generation is 28.2 GWh in the course of that 7.2 hours, or 3.92
GW. The throughput of the storage system is more than 7500 GWh annually.
By a similar course of reasoning, in an intermediate case where the wind
machines operate 60% of the time, with an occupancy factor of 0.5, then the
amount to be stored is (9.6 / 0.8) or 12 GWh ; over 14.4 hours,
then, a generation of 26.4 GWh requires an installed capacity of
(1.833 / 0.5) or 3.67 GW. In this case, the storage scheme handles
about 4400 GWh each year. And if the wind machines run at 30% power 100% of
the time, no storage is needed, there are no storage losses, and 24 GWh daily
is supplied by generating 24 GW continuously from (1000 / 0.3) or
3.33 GW of installed capacity.
For an idea of the scale of the necessary works, we may observe that the
installed capacity of Hoover Dam is 2080 MW, and its annual generation is
about 4200 GWh.
…but they do not
displace fossil fuels.
According to David Tolley, in a keynote address delivered to the
Institution of Mechanical Engineers (of Great Britain), 15 January 2003 :
When plant is de-loaded to balance the system, it results in a significant proportion of deloaded plant which operates relatively inefficiently. … Coal plant will be part-loaded such that the loss of a generating unit can swiftly be replaced by bringing other units on to full load. In addition to increased costs of holding reserve in this manner, it has been estimated that the entire benefit of reduced emissions from the renewables programme has been negated by the increased emissions from part-loaded plant under NETA.
A very clear illustration of the problem is given by what the California Independent System Operator, which has to cope with some 4 GW of photovoltaic capacity, has taken to calling the duck curve. As can be seen, the heaviest load of the day comes onto the system just as solar output is going off, requiring rapid increases of other generation. It is scarcely obvious, either how a material reduction in fossil fuel use can be expected, or what justifies the expenditure of money to obtain this sort of result.
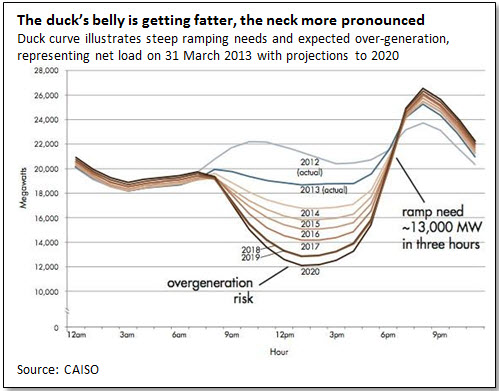
Sources
Hyperlinks in the text generally point to resources the present author found particularly edifying or apposite to the subject at hand, rather than those which he principally drew upon in preparing the article. In some cases they have been selected precisely because their viewpoint differs strongly from that expressed in these pages, but they nevertheless present the relevant facts.
For basic data, frequent reference was made to the CRC Handbook of Chemistry and Physics, 56th Edition, 1975—1976 (Robert Weast, ed ; Cleveland : CRC Press), especially to the Table of the Isotopes, pp B-253—B-336. Much material related to nuclear reactors and fuels relies on Richard Stephenson, Introduction to Nuclear Engineering (2d edn ; New York : McGraw-Hill, 1958), Raymond Murray, Introduction to Nuclear Engineering (2d edn ; Englewood Cliffs, NJ : Prentice-Hall, 1961), and Samuel Glasstone, Sourcebook on Atomic Energy (2d edn ; Princeton, NJ : D. Van Nostrand, 1958) ; the first editions of all three books are less useful, because much material on the subject was declassified only with the Geneva Conference of 1955.
The “atomic fist” logo is adapted from an image found in variations on free clip-art sites, and purported to be in the public domain. Metadata connect the original with a user known as Tweenk. Inference suggests that this is the same person as a Redditor by the same alias, who may be Krzysztof Kosiński of Warsaw.
